水頭の概念

　流管内の定常流に関しては、水理学の基本定理であるベルヌーイ(Bernoulli)の定理が成り立ちます(この時、粘性を考慮しない)。

[ ( γ_w × v² ) / ( 2 × g ) ] + [ γ_w ] × [ z ] + u = 一定　・・・(式1)

ここに、
　γ_w：液体の単位体積重量 ( kN / m³ )
　v ：液体の流速 ( m / sec )
　g　：重力加速度 ( m / sec² )
　z ：標高 ( m )
　u ：圧力 (液圧) ( kN / m² )

　(式1)において、左辺第1項：[ ( γw × v2 ) / ( 2 × g ) ]は運動エネルギー、第2項：[ γw ]は位置エネルギー、第3項：[ z ]は圧力エネルギーを示し、これらの総和は一定となります。

　(式1)の両辺をγwで割ると、下式になります。

[ v2 / 2 × g ] + [ z ] + [ u / γw ] = 一定・・・(式2)

　この時、土中においては流速vは非常に小さいため、v2=0とみなすことができます。

[ z ] + [ u / γw ] = 一定・・・(式3)

　左辺の各項は高さの次元であるため、hとして表現します。

h = [ z ] + [ u / γw ] = 一定・・・(式4)

　z = he、u / γw = hp とすると

h = he + hp

　となります。ここで、hを全水頭、heを位置水頭、hpを圧力水頭と呼びます。これらはすべて長さの次元を有します。

水頭を用いた土中の透水の検討

　水頭の概念を用いることで、土中の透水の様相を要領よく把握することができます。下図のモデルで検討します。

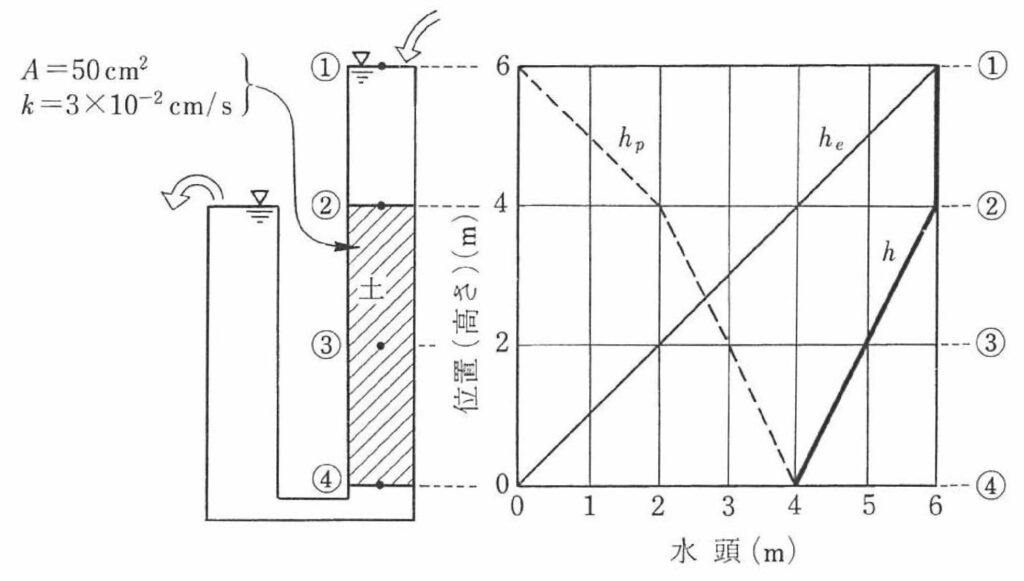
　図の土（斜線部）を水が透水するときの、土中の水の動きを考えます。即ち、各位置における水頭を求めます。求め方は次の通りです。

1) 　①～④各点の位置水頭h_eを求めます。位置水頭は高さ基準点(=0)からの高さとなります。高さの基準は任意ですが、ここでは土試料の最下点とします。
　h_e1=6.0m、h_e2=4.0m、h_e3=2.0m、h_e4=0.0m
2)　①～④各点の圧力水頭h_Pを求めます。圧力水頭はその位置にかかる水圧に等しく、大気圧に接する面からの高さとなります。この時、土中の圧力水頭は直接求めません。
　hP1=0.0m、hP2=2.0m、hP3=(後に求めます)、hP4=4.0m
　④における大気圧に接する面からの高さは、流下側からの高さを取ります。
3)　土中の圧力水頭h_P(ここでは位置③)を求めます。右グラフにおける土試料の両端②④の圧力水頭を直線で結び、h_e3との交点がh_P3となります（グラフh_P3水頭=3.0m）
4)　①～④各点の全水頭hを求めます。全水頭は各高さにおける位置水頭h_eと圧力水頭h_Pの和に等しくなります。

以上が、土中の水頭の求め方です。水頭の概念を用いた土中の透水に関しては、次のような留意点が挙げられます。

1)　全水頭は土中においてのみ変化する（=土中では、全水頭が変化する）。
2)　水は全水頭の大きいところから小さいところに向かって流れる。
3)　等質・等断面の土中では、全水頭は一定の割合で変化する（等質・等断面：kやAが一定）。
4)　位置水頭の基準点は任意に設定してよい。
5)　圧力水頭は負の値をとりうる（このため、上グラフ横軸は本来左に負の値まで取るべき）。